2022-02-12

cosXの微分が―sinXになる理由、気になりませんか？

数学

cosXを微分すると-sinXになるのはどうしてでしょうか。

気になりますよね。

はやる気持ちを抑えつつ一緒に見ていきましょう。

まずは和積公式を使った証明です。

cosXの微分

$\displaystyle\lim_{h \to 0}\frac{cos(x+h)-cos\,x}{h}$

を求めるために次の和積公式を使います

$\displaystyle\ cosA-cosB=-2sin\frac{A+B}{2}sin\frac{A-B}{2}$

この公式で $A=x+h,B=x$ とすると

$\displaystyle\frac{A+B}{2}=\frac{2x+h}{2}=x+\frac{h}{2}$

$\displaystyle\frac{A-B}{2}=\frac{h}{2}$ なので

$\displaystyle\lim_{h \to 0}\frac{cos(x+h)-cos\,x}{h}$

$\displaystyle\ =\lim_{h \to 0}\frac{-2sin(x+\frac{h}{2})sin\frac{h}{2}}{h}$

$\displaystyle\ =\lim_{h \to 0}-sin(x+\frac{h}{2})\frac{sin\frac{h}{2}}{\frac{h}{2}}$

ここで

$\displaystyle\lim_{h \to 0}sin(x+\frac{h}{2})=sin\,x$

$\displaystyle\lim_{h \to 0}\frac{sin\frac{h}{2}}{\frac{h}{2}}=1$ なので

(なぜなら $\displaystyle\lim_{t \to 0}\frac{sin\,t}{t}=1$ だから)

$\displaystyle\lim_{h \to 0}-sin(x+\frac{h}{2})\frac{sin\frac{h}{2}}{\frac{h}{2}}$

$=-sin\,x\cdot1$

$=-sin\,x$ となります

よって $cos\,x$ を微分すると $-sin\,x$ になることが証明できました

今一度振り返ってみると和積公式にうまく当てはめ極限の公式も使いながら証明していましたね。

ただ、みなさんの中には和積公式なんてすっかり忘れちゃったしどうやって導けばいいのかわからないよという方もいるのではないでしょうか。

そんな方はぜひともこちらのページをご覧ください。

ecole2.hatenablog.com

和積公式、それから積和公式の導き方までわかっちゃいます。

和積公式や積和公式というのはついつい忘れがちになってしまいそうですがたまに使うことがあるので、もしかしたらこの問題で使うかもという気持ちを持っておきたいところですね。

それではお待たせしました、いよいよ2つ目の証明に参りましょう。

今度は加法定理を使った証明になります。

$\displaystyle\lim_{h \to 0}\frac{cos(x+h)-cos\,x}{h}$ で

$cos(x+h)$ は加法定理により

$=cos\,x\,cos\,h-sin\,x\,sin\,h$ なので

$\displaystyle\frac{cos(x+h)-cos\,x}{h}$

$\displaystyle =\frac{cos\,x\,cos\,h-sin\,x\,sin\,h-cos\,x}{h}$

$\displaystyle =\frac{cos\,x(cos\,h-1)-sin\,x\,sin\,h}{h}$

よって

$\displaystyle\frac{d}{dx}cos\,x$

$\displaystyle =\lim_{h \to 0}(\frac{cos\,x(cos\,h-1)}{h}-\frac{sin\,x\,sin\,h}{h})$

となるわけですが、ここで

$\displaystyle\lim_{h \to 0}\frac{(cos\,h-1)}{h}$

$\displaystyle =\lim_{h \to 0}\frac{-(1-cos\,h)}{h^{2}}\cdot{h}$ について

$\displaystyle\lim_{h \to 0}\frac{-(1-cos\,h)}{h^{2}}=-\frac{1}{2}$

$\displaystyle\lim_{h \to 0}h=0$ であり

一方で $\displaystyle\lim_{h \to 0}\frac{sin\,h}{h}=1$ なので

$\displaystyle\lim_{h \to 0}(\frac{cos\,x(cos\,h-1)}{h}-\frac{sin\,x\,sin\,h}{h})$

$\displaystyle =cos\,x\cdot{\frac{-1}{2}}\cdot0-sin\,x\cdot1$

$\displaystyle =-sin\,x$

となって証明できました

今の証明を振り返ってみると微分の式に加法定理をうまいこと当てはめてそのあと極限の公式を使うという流れでしたね。

極限の公式を使うところは難しく感じた方もいるかもしれません。

ぜひとも落ち着いて理解していきましょう。

さて、三角関数というのは学べば学ぶほどいろいろと役に立つものです。

もっと学びたい方にはこちらのページがおすすめです。

ecole2.hatenablog.com

基本的でありながら重要な内容となっていますのでぜひご覧ください。それでは今回はこの辺で。

2022-02-05

sinXの微分はなぜcosXになるのか？

数学

微積分でsinXの微分がcosXになるのはどうしてでしょうか。

さっそくその秘密を見ていきましょう。

sinの微分

$\displaystyle\lim_{h \to 0}\frac{sin(x+h)-sin\,x}{h}$

を求めるために次の和積公式を使います

$\displaystyle\ sinA-sinB=2cos\frac{A+B}{2}sin\frac{A-B}{2}$

この公式で $A=x+h,B=x$ とすると

$\displaystyle\frac{A+B}{2}=\frac{2x+h}{2}=x+\frac{h}{2}$

$\displaystyle\frac{A-B}{2}=\frac{h}{2}$ なので

$\displaystyle\lim_{h \to 0}\frac{sin(x+h)-sin\,x}{h}$

$\displaystyle\ =\lim_{h \to 0}\frac{2cos(x+\frac{h}{2})sin\frac{h}{2}}{h}$

$\displaystyle\ =\lim_{h \to 0}cos(x+\frac{h}{2})\frac{sin\frac{h}{2}}{\frac{h}{2}}$

ここで

$\displaystyle\lim_{h \to 0}cos(x+\frac{h}{2})=cos\,x$

$\displaystyle\lim_{h \to 0}\frac{sin\frac{h}{2}}{\frac{h}{2}}=1$ なので

(なぜなら $\displaystyle\lim_{t \to 0}\frac{sin\,t}{t}=1$ だから)

$\displaystyle\lim_{h \to 0}cos(x+\frac{h}{2})\frac{sin\frac{h}{2}}{\frac{h}{2}}$

$=cos\,x\cdot1$

$=cos\,x$ となります

よって $sin\,x$ を微分すると $cos\,x$ になることが証明できました

こんなふうに和積公式をうまく使うことで証明していましたね。

続いて2つめの証明方法なのですが今度は加法定理を使います。

それでは見ていきましょう。

$\displaystyle\lim_{h \to 0}\frac{sin(x+h)-sin\,x}{h}$ で

$sin(x+h)$ は加法定理により

$sin\,x\,cos\,h+cos\,x\,sin\,h$ なので

$\displaystyle\frac{sin(x+h)-sin\,x}{h}$

$\displaystyle =\frac{sin\,x\,cos\,h+cos\,x\,sin\,h-sin\,x}{h}$

$\displaystyle =\frac{sin\,x(cos\,h-1)+cos\,x\,sin\,h}{h}$

よって

$\displaystyle\frac{d}{dx}sin\,x$

$\displaystyle =\lim_{h \to 0}(\frac{sin\,x(cos\,h-1)}{h}+\frac{cos\,x\,sin\,h}{h})$

となるわけですが、ここで

$\displaystyle\lim_{h \to 0}\frac{(cos\,h-1)}{h}$

$\displaystyle =\lim_{h \to 0}\frac{-(1-cos\,h)}{h^{2}}\cdot{h}$ について

$\displaystyle\lim_{h \to 0}\frac{-(1-cos\,h)}{h^{2}}=-\frac{1}{2}$

$\displaystyle\lim_{h \to 0}h=0$ であり

一方で $\displaystyle\lim_{h \to 0}\frac{sin\,h}{h}=1$ なので

$\displaystyle\lim_{h \to 0}(\frac{sin\,x(cos\,h-1)}{h}+\frac{cos\,x\,sin\,h}{h})$

$\displaystyle =sin\,x\cdot{\frac{-1}{2}}\cdot0+cos\,x\cdot1$

$\displaystyle =cos\,x$

となって証明できました

以上のように2通りの方法でsinXの微分がcosXになる理由を証明できたわけなのですがどうだったでしょうか。

ここまで読んできた方はもっと三角関数について知りたくなったのではないでしょうか。

そんな方はぜひこちらのページをご覧ください

ecole2.hatenablog.com

三角関数の方程式についてのページなのですが今回学んだ微分の内容と合わせて学習すれば三角関数についての理解がより一層深まること間違いなしです。

そして様々な式変形について上達することで三角関数の出てくる問題をどんどん解けるようになっていっていただければ幸いです。

2018-12-27

三角関数の2倍角の公式、3倍角の公式の証明

数学

今回は2倍角の公式、3倍角の公式についてです。

まず、2倍角の公式は次のようになります。

$sin2X=2sinXcosX$

$cos2X=2cos^{2}X-1=1-2sin^{2}X$

$\displaystyle\ tan2X=\frac{2tanX}{1-tan^{2}X}$

そして、3倍角の公式は以下の式です。

$sin3X=3sinX-4sin^{3}X$

$cos3X=4cos^{3}X-3cosX$

では2倍角の公式から証明していきたいと思います。

まず、sinの加法定理の式

$sin(P+Q)=sinPcosQ+cosPsinQ$

において $P=Q=X$ 　として

$sin2X=sinXcosX+cosXsinX$

$=2sinXcosX$

また、cosの加法定理の式

$cos(P+Q)=cosPcosQ-sinPsinQ$

において $P=Q=X$ 　として

$cos2X=cosXcosX-sinXsinX$

$=cos^{2}X-sin^{2}X$

$=cos^{2}X-(1-cos^{2}X)$

$=2cos^{2}X-1$

$=2(1-sin^{2}X)-1$

$=1-2sin^{2}X$

そして、tanの加法定理の式

$\displaystyle\ tan(P+Q)=\frac{tanP+tanQ}{1-tanPtanQ}$

において $P=Q=X$ 　として

$\displaystyle\ tan2X=\frac{2tanX}{1-tan^{2}X}$

続いて3倍角の公式を示したいと思います。

sinの加法定理の式

$sin(P+Q)=sinPcosQ+cosPsinQ$

において $P=2X,Q=X$ 　として

$sin3X=sin2XcosX+cos2XsinX$

$=2sinXcos^{2}X+(1-2sin^{2}X)sinX$

$=2sinX(1-sin^{2}X)+sinX-2sin^{3}X$

$=2sinX-2sin^{3}X+sinX-2sin^{3}X$

$=3sinX-4sin^{3}X$

また、cosの加法定理の式

$cos(P+Q)=cosPcosQ-sinPsinQ$

において $P=2X,Q=X$ 　として

$cos3X=cos2XcosX-sin2XsinX$

$=(2cos^{2}X-1)cosX-2sin^{2}XcosX$

$=2cos^{3}X-cosX-2(1-cos^{2}X)cosX$

$=2cos^{3}X-cosX-2cosX+2cos^{3}X$

$=4cos^{3}X-3cosX$

以上により2倍角、3倍角の公式が証明されました。

三角関数の2倍角、3倍角の公式はsinやcosの出てくる方程式や不等式の問題を解くときに使うことが多いですが、積分を用いて面積や体積を求める問題を解くときにも式変形などで非常に役に立ちます。

特に2倍角のほうはよく使うのでぜひとも覚えておきたいのですが、忘れてしまったときでもどのように導くかがわかっていれば公式を作れますね。

2倍角の公式、3倍角の公式はどちらも証明するためには加法定理を使ったのでした。

さて、もっと数学の力をつけたい方は次の動画を見てみましょう。

いい問題です。

www.youtube.com

2018-12-25

積和公式と和積公式の証明はこれでばっちりわかります！

数学

まず積和公式とは何かと言いますと、以下のような式になります。

$\displaystyle\ sinPcosQ＝\frac{sin(P＋Q)＋sin(P－Q)}{2}$

$\displaystyle\ cosPcosQ＝\frac{cos(P＋Q)＋cos(P－Q)}{2}$

$\displaystyle\ sinPsinQ＝-\frac{cos(P＋Q)＋cos(P－Q)}{2}$

これらを証明するために加法定理を使います。

加法定理は以下の（1）から（4）の式ですが

(1) $sin(P＋Q)＝sinPcosQ＋cosPsinQ$

(2) $sin(P－Q)＝sinPcosQ－cosPsinQ$

(3) $cos(P＋Q)＝cosPcosQ－sinPsinQ$

(4) $cos(P－Q)＝cosPcosQ＋sinPsinQ$

ここで、（1）と（2）を足して

(5) $sin(P＋Q)＋sin(P－Q)＝2sinPcosQ$

$\displaystyle\ sinPcosQ＝\frac{sin(P＋Q)＋sin(P－Q)}{2}$

また、（3）と（4）を足して

(6) $cos(P＋Q)＋cos(P－Q)＝2cosPcosQ$

$\displaystyle\ cosPcosQ＝\frac{cos(P＋Q)＋cos(P－Q)}{2}$

今度は、（3）から（4）を引いて

(7) $cos(P＋Q)－cos(P－Q)＝－2sinPsinQ$

$\displaystyle\ sinPsinQ＝-\frac{cos(P＋Q)-cos(P－Q)}{2}$

以上により示されました。

続いて和積公式とは次のような式で

$\displaystyle\ sinX+sinY=2sin\frac{X+Y}{2}cos\frac{X-Y}{2}$

$\displaystyle\ sinX-sinY=2cos\frac{X+Y}{2}sin\frac{X-Y}{2}$

$\displaystyle\ cosX-cosY=-2sin\frac{X+Y}{2}sin\frac{X-Y}{2}$

$\displaystyle\ sinX-sinY=2cos\frac{X+Y}{2}sin\frac{X-Y}{2}$

これらの証明にも加法定理を使います。

$P＋Q＝X、P-Q＝Y$ 　とすると

$\displaystyle\ P＝\frac{X＋Y}{2}、Q＝\frac{X-Y}{2}$ 　なので

（5）より

$\displaystyle\ sinX+sinY=2sin\frac{X+Y}{2}cos\frac{X-Y}{2}$

（6）より

$\displaystyle\ cosX+cosY=2cos\frac{X+Y}{2}cos\frac{X-Y}{2}$

（7）より

$\displaystyle\ cosX-cosY=-2sin\frac{X+Y}{2}sin\frac{X-Y}{2}$

また、（1）から（2）を引くと

$sin(P＋Q)－sin(P－Q)＝2cosPsinQ$ なので

$\displaystyle\ sinX-sinY=2cos\frac{X+Y}{2}sin\frac{X-Y}{2}$

以上により示されました。

積和公式や和積公式は三角関数で学ぶ他の重要な定理、例えば正弦定理や余弦定理、加法定理といったものに比べると使う機会が少ないこともあってか忘れられがちです。

しかし問題によっては使うこともあるので忘れずに意識しておきたい公式ではあります。

そしてこれらの公式は覚えていることよりも導き方を知っていることの方が大切だと思います。

実際、積和公式や和積公式というのは加法定理を使って求めることができたのですね。

加法定理は三角関数を使った数学の問題を解くときによく利用する定理だと思いますがこの加法定理をうまく当てはめることで今回求めたい公式へとつながりました。

このように知っている定理をちょっとひと工夫するだけで一気に視界が開けて解決策が見えてくるというのは数学の問題でよくあることです。

今回はそんな一例を実感していただけたのではないでしょうか。

さて、ここまで読んできた方は数学力をもっと高めたくなったのではないでしょうか。

そんな方には次の動画がおすすめです。三角関数の力が向上すること間違いなしです。

この動画ですが、ただ単にタイトルが英語になっているだけで再生すれば英語は出てきません。なのでどなたでもご覧ください。

www.youtube.com

2018-12-10

旧帝大や金岡千広を受ける人向けの分数の漸化式の数列問題

数学

今回は分数の漸化式の問題です。

複雑に見えますが落ち着いて見ていくことが大切です。

特に旧帝大や金岡千広クラスの大学を受験するなら解いておいて損ではない問題です。

[問題] nを自然数として次のような条件で数列が与えられたとする。

$\displaystyle\ a_{n+1}=\frac{3a_n+2}{2a_n+6}$ 　 $,$ 　 $a_1=3$

このとき

(1)すべての自然数nに対して $a_n\neq-2$ であることを示せ

(2) $\displaystyle\ b_n=\frac {2a_n-1} {2a_n + 4}$ とするとき { $b_n$ }の漸化式を求めよ

(3) 数列 { $a_n$ }の一般項を求めよ

[解答]

（1）あるnで $a_n=-2$ になったとすると

$\displaystyle\ a_n=\frac{3a_{n-1}+2}{2a_{n-1}+6}$ なので

$\displaystyle\ -2=\frac{3a_{n-1}+2}{2a_{n-1}+6}$

$-4a_{n-1}-12=3a_{n-1}+2$

$7a_{n-1}=-14$ 　、 $a_{n-1}=-2$

となってこれを繰り返すことで

$a_{n-1}=-2$ 、‥‥、 $a_1=-2$

となり $a_1=3$ に矛盾する。

よって、すべての自然数nに対して $a_n\neq-2$ である

（2） $\displaystyle\ b_{n+1}=\frac{2a_{n+1}-1}{2a_{n+1}+4}$

$\displaystyle\ =\frac{2\frac{3a_n+2}{2a_n+6}-1}{2\frac{3a_n+2}{2a_n+6}+4}$

$\displaystyle\ =\frac{2(3a_n+2)-(2a_n+6)}{2(3a_n+2)+4(2a_n+6)}$

$\displaystyle\ =\frac{6a_n+4-2a_n-6}{6a_n+4+8a_n+24}$

$\displaystyle\ =\frac{4a_n-2}{14a_n+28}$

$\displaystyle\ =\frac{2(2a_n-1)}{7(2a_n+4)}$

よって $\displaystyle\ b_{n+1}=\frac{2}{7}b_n$

（3） $\displaystyle\ b_1=\frac{2a_1-1}{2a_1+4}$

$\displaystyle\ =\frac{2\cdot{3}-1}{2\cdot{3}+4}=\frac{5}{10}=\frac{1}{2}$

なので $\displaystyle\ b_n=\frac{1}{2}\cdot{(\frac{2}{7})^{n-1}}$

$\displaystyle\frac{1}{2}\cdot{(\frac{2}{7})^{n-1}}=\frac{2a_{n+1}-1}{2a_{n+1}+4}$

$\displaystyle\ (\frac{2}{7})^{n-1}=\frac{2a_{n+1}-1}{a_{n+1}+2}$

$\displaystyle\ (a_n+2)(\frac{2}{7})^{n-1}=2a_n-1$

$\displaystyle\ (2-(\frac{2}{7})^{n-1})a_n=1+2\cdot{(\frac{2}{7})^{n-1}}$

$\displaystyle\frac{2\cdot{7^{n-1}}-2^{n-1}}{7^{n-1}}a_n=\frac{7^{n-1}+2^{n}}{7^{n-1}}$

$\displaystyle\ a_n=\frac{7^{n-1}+2^{n}}{2\cdot{7^{n-1}}-2^{n-1}}$

$a_{n}$ とは別に $b_{n}$ についての漸化式を作ることで問題を解いたのですね。

2018-12-05

正弦定理と加法定理を使って余弦定理の式を求める

数学

三角関数の代表的な定理のひとつである余弦定理ですが、今回は正弦定理と加法定理を使って余弦定理の式を求めてみたいと思います。

f:id:ecole2:20181204091003j:plain

余弦定理の式は

$c^2=a^2+b^2-2ab\cdot{cosC}$

ですが、これを変形した

$a^2+b^2-c^2=2ab\cdot{cosC}$

を求めたいと思います。まず正弦定理より

$\displaystyle\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$

（Rは三角形ABCの外接円の半径）

ここで 2R = kとおくと

a＝ksinA、b＝ksinB、c＝ksinC　となるので

$a^2+b^2-c^2$

$=(ksinA)^2+(ksinB)^2-(ksinC)^2$

$=k^2(sin^2A+sin^2B-sin^2C)$

ここで、C＝180°－(A＋B)　なので

sinC＝sin{180°－(A＋B)}＝sin(A＋B)

＝sinAcosB＋cosAsinB (加法定理)

$sin^2C=(sinAcosB+cosAsinB)^2$

$=sin^2Acos^2B+cos^2Asin^2B$

$+2sinAcosBcosAsinB$

この結果を先ほどの式に代入して

$a^2+b^2-c^2$

$=k^2(sin^2A+sin^2B-sin^2Acos^2B-$

$cos^2Asin^2B-2sinAcosAsinBcosB)$

かっこの中を計算すると

$sin^2A(1-cos^2B)+sin^2B(1-cos^2A)$

$-2sinAcosAsinBcosB$

$=sin^2Asin^2B+sin^2Bsin^2A$

$-2sinAcosAsinBcosB$

$=2sinAsinB\times$

$(sinAsinB-cosAcosB)$

$=-2sinAsinBcos(A+B)$

よって

$a^2+b^2-c^2$

$=-2k^2sinAsinBcos(A+B)$

$=-2ab\cdot{cos(A+B)}$

$=-2ab\cdot{cos(180°-C)}$

$=2ab\cdot{cosC}$

もっと数学の実力を伸ばしたいという方は次の動画を見てみましょう。

www.youtube.com

2018-12-03

角の二等分線定理にこんな面白い証明があるって知ってました？

数学

三角形があってその中の1つの角を二等分する線が引かれているとき角の二等分線定理が役立つことが大いにあります。そんな角の二等分線定理とはいったいどのような定理かと言いますと、

f:id:ecole2:20181203060830j:plain

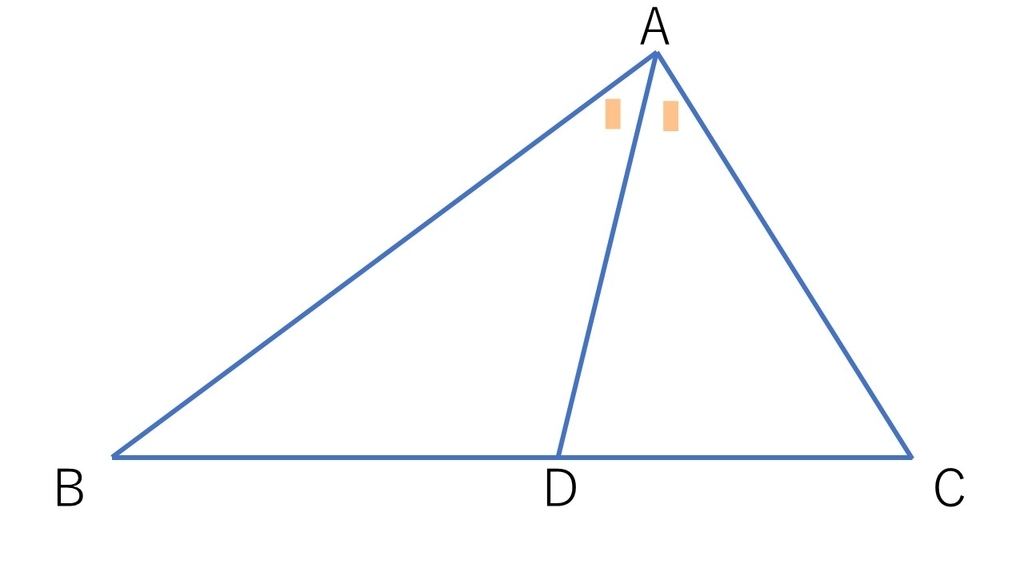
三角形ABCがあって∠BAD＝∠CADとなるようにBC上に点Dをとるとき、

AB:AC = BD:CD

が成り立つという定理です。この定理を使って図形の問題を解くという場面は結構よく出てくるので角の二等分線定理は知ってる、使ったことがあるという方も多いのではないでしょうか。今回はそんな角の二等分線定理の面白い証明をご紹介したいと思います。まずは三角形の相似を使った証明です。

直線ADに対して点B、Cから垂線を下ろし、直線ADとの交点をそれぞれP、Qとします。

f:id:ecole2:20181203061435j:plain

このとき、∠BAP＝∠CAQ、∠BPA＝∠CQA　なので三角形ABPと三角形ACQは相似となります。よって、AB：AC＝BP：CQ

一方で∠BDP＝∠CDQ、∠BPD＝∠CQD　なので三角形BDPと三角形CDQは相似です。よってBP：CQ＝BD：CD

以上によりAB：AC＝BD：CDとなります。

今の証明は三角形の相似を2回使うことがポイントでした。では続いて三角形の面積に着目した証明を見てみましょう。点DからAB、ACにそれぞれ垂線を下ろし交点をE、Fとします。

f:id:ecole2:20181203065449j:plain

このとき∠DEA＝∠DFA＝90°、∠DAE＝∠DAF、DAは共通で、「直角三角形で斜辺とひとつの角が等しければ合同」なので三角形DAEと三角形DAFは合同となります。よってDE＝DF。さて、ここで三角形ABDと三角形ACDの面積比を考えたいと思います。

f:id:ecole2:20181203065449j:plain

まず、AB、ACをそれぞれ底辺とみたとき△ABD＝AB・DE・1/2で、△ACD＝AC・DF・1/2ですがDE＝DFなので△ABD：△ACD＝AB：AC。一方でBDとCDを底辺とみたとき高さは共通なので△ABD：△ACD＝BD：CD。以上によりAB：AC＝BD：CDとなります。

続いて以下のyoutube動画に進みましょう。

https://youtu.be/q6Q-I32jFg8

ここまで角の二等分線定理の証明を行ってまいりました。

直角三角形の相似を考えたり合同を考えたりしてどのような直角三角形を作るのかが異なっているのが注目すべきポイントだと思います。

このように図形の問題ではどのような観点から見るかによって使うべき道具も様々で、そのことがいろいろな数学の問題を解いていく上での醍醐味といえるのではないでしょうか。

同じような醍醐味を得られるものとしてはチェバの定理の証明もあります。

この証明も今回の角の二等分線定理と同様に異なる観点から考えていくことで定理そのものをより一層理解することができるようになっています。

非常に面白い証明だと思いますのでぜひこちらのページをご参照ください。

チェバの定理の証明します、2通りで！ - 学びをつづる

また、図形の問題では三角関数を使った計算と相似などの性質を組み合わせて解いていくことがよくありますが、そうしたときに知っておくと役立つ定理としましてはまず正弦定理があります。

図形の学習を行う上で基本的な定理となるわけですがそんな正弦定理がどういった定理なのか、また正弦定理の証明はどのように行えばよいのかについては下のページが参考になることと思います。

正弦定理の証明がわかります！ - 学びをつづる

そのほかに役立つ公式といたしましては2倍角の公式、3倍角の公式も挙げられます。

こちらの公式はどのようなものかと言いますと、角度が2倍や3倍になったときに三角関数の計算をスムーズに行うことができる公式となっています。

3倍角の公式はたまに使うことがあるかなという感じですが2倍角の公式は数学の問題を解いていく上で結構頻繁に出てきて図形の問題はもちろん計算主体の問題などいろいろ場面に応用可能な公式ですのでぜひとも下のページをご参照ください。

角の二等分線定理や正弦定理と同じく、公式そのものを知るだけではなく証明も合わせて学習することで公式を理解しやすくなると思いますのでとてもためになるはずです。

三角関数の2倍角の公式、3倍角の公式の証明 - 学びをつづる

今回は角の二等分線定理というまさに図形について考えていたわけですが、こうした図形の問題を解いていく上では数式の計算問題の学習も重要です。

なぜなら図形の問題ではしばしば辺の長さや面積を求めよという問いが出題されますが、そうした場面において数式の計算を正確に行えるかどうかによって正しい答えが導けたり問題を解くスピードをアップさせたりすることができるからです。